Что такое агронавигатор?
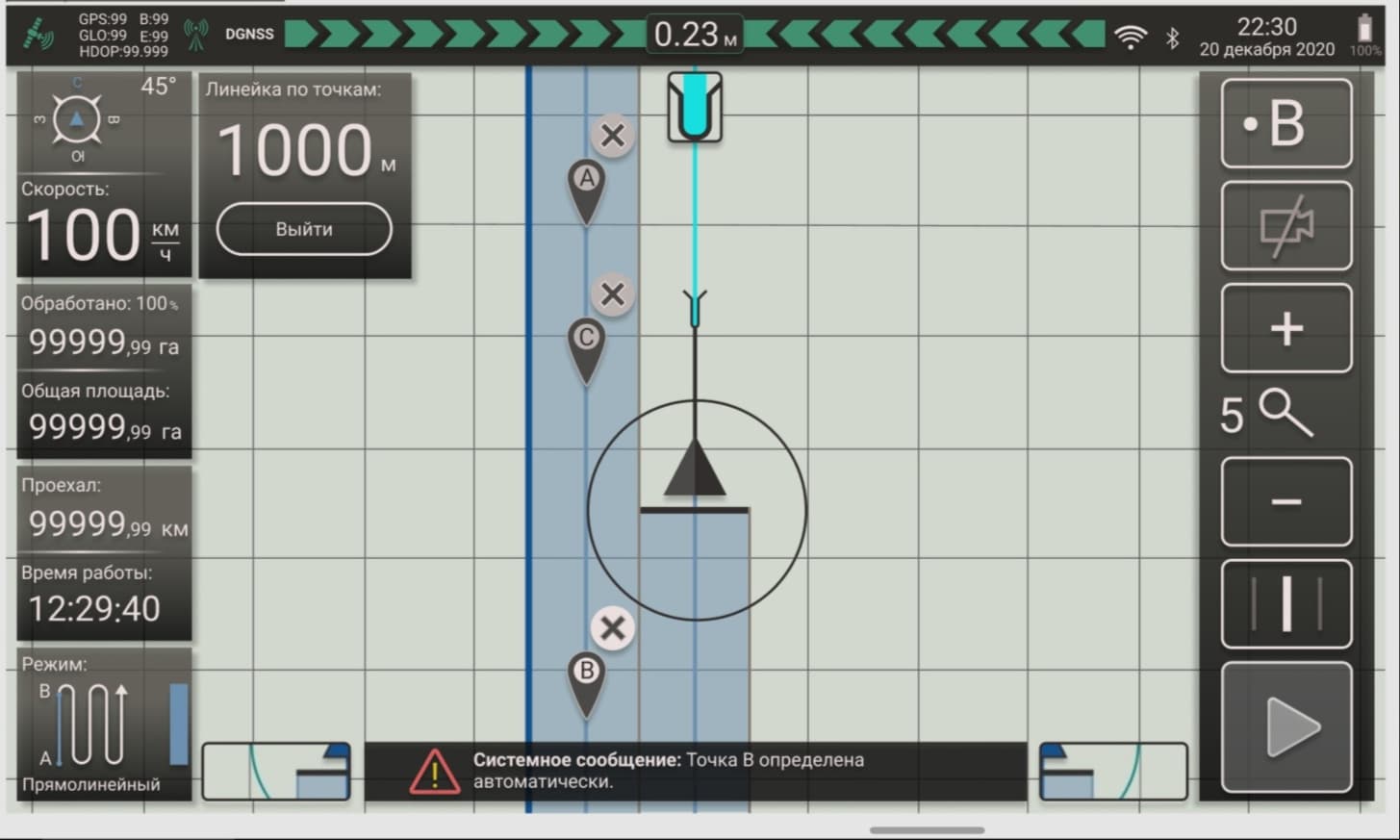
Причем тут математика?
Как вы знаете, навигатор (любой) ориентируется в пространстве благодаря спутниковому сигналу. Но сигнал со спутника приходит с определенной погрешностью. Да, в инструкции говорится, что все в пределах нормы, но если вы неверно подключили антенну или с ней возникли проблемы - появляются погрешности. Из-за них стоящее неподвижно устройство постоянно получает разные координаты своего местоположения, поэтому на экране оно отображается некорректно - как будто постоянно "прыгает" на месте. Чтобы этого избежать и чтобы правильно описать кривую движения по точкам, мы применяем линейную регрессию из методов машинного обучения.
В нашем гипотетическом поле трактор может вытворять всякие необычные вещи. Например, он может тянуть за собой прицеп: тележку, сеялку, опрыскиватель и т.д., движение которых мы обязаны отслеживать, поскольку именно они выполняют полевую работу (например, разбрасывают семена). Но! Планшет с приложением по-прежнему как стоял, так и стоит на тракторе. А траекторию агронавигатор должен учитывать с точки зрения самого прицепного оборудования. При различных разворотах пути "трактора" и "сеялки" будут отличаться. Поэтому здесь мы решаем нетривиальную задачу: как по маршруту движения агрегата определить маршрут движения прицепа? Без знания математики и механики - да никак!
Отображение агрегата и прицепа в настройках приложения
При отображении траектории движения агрегата в приложении (хоть с прицепом, хоть без него) тоже возникает много вопросов "как?". Если мы просто напрямую отрисовываем маршрут на экране, то количество точек этого маршрута постоянно растет и в конце концов становится очень велико (например, в течении дня трактор работает около 12 часов - и все эти точки фиксируются в нашем агронавигаторе). Отрисовав всю эту массу как есть, "в лоб", мы получим серьезную проблему: количество точек негативно скажется на производительности. Здесь перед нами алгоритм линейной сложности: количество отображаемых кадров в единицу времени заметно падает по мере роста количества точек - и в итоге мы начнем показывать менее одного кадра в секунду (только представьте, как при этом будет выглядеть работа приложения!). Для решения проблемы нужна структура данных, которая позволит в один момент времени строить только конечную часть маршрута нашего трактора, чтобы поддерживать одну и ту же скорость отрисовки на экране. Давайте поговорим об этом поподробнее. Как вы понимаете, наша задача состоит в том, чтобы формировать изображение на планшете и желательно делать это по 60 раз за секунду. Но, если мы рисуем точки непрерывно, это занимает все больше и больше времени. Рано или поздно количество времени на отрисовку точек становится больше, чем мы можем заложить на отрисовку 1 кадра. Чтобы с этим справиться, применяются алгоритмы и структуры данных, которые позволяют отображать только ту часть маршрута, которая нужна нам на экране вот прямо сейчас. За счет этого, количество "экранных" точек в каждый момент времени не растет, оно остается примерно одинаковым. Но для реализации этого решения необходимо знание алгоритмов и структур данных, нужно выбрать такую структуру, которая позволит выбирать только нужные нам точки маршрута, которые мы в данный момент хотим показать. Как? Каждая точка попадает в какой-то определенный квадрант - и мы формируем их список по каждому квадранту. А затем из массива, допустим в 10 000 точек, выбираем только те, которые находятся в нужном квадранте - а не все подряд. Предполагается, что водитель агрегата не будет намеренно проезжать много раз по одному и тому же месту - и не создаст нам кучу "лишних" точек в одном квадранте. Кроме того, в данном случае нам пригождается канторовская нумерационная функция и ее вариации - преобразование таблички в сплошной массив и обратно невозможно без нее. Это основа основ, ее обязательно нужно знать для работы с квадрантами.
Еще пара крайне важных математических решений для агронавигатора - это алгоритм поиска пересечений и алгоритм поиска островов. Поиск пересечений маршрута - то есть, тех мест, где агрегат проехал повторно - невозможен без математики. Как определить, например, что два треугольника пересекаются и узнать площадь пересечения? Здесь мы используем определение пересечения линий из геометрии. В данном случае мы берем стороны каждой фигуры, составляем уравнение прямой по двум точкам и находим точки пересечения линий. Также нам необходимо найти те участки, которые вообще не были обработаны. Как узнать их площадь при том, что мы даже не видим точной границы нашего поля? Здесь мы говорим, что то, что находится "внутри" наших траекторий движения агрегата является "пропуском". Чтобы находить пропуски, мы решили использовать алгоритм поиска островов - он достаточно трудоемкий, но, к счастью, его применение не очень часто требуется при разработке приложения. Для нечастого запуска и размеров наших полей он подходит даже при условии своей большой сложности. Жизненно важно обращать внимание на построение системы координат: мы не всегда стартуем из идеальной точки "ноль", координаты нашего трактора могут быть и отрицательными. Но, чтобы "запихнуть" их в алгоритм островов, придется перейти к другой системе координат - к относительной. Тогда алгоритм заработает - и эта задача тоже требует от разработчика в первую очередь математических познаний.
Алгоритм Брезенхема - алгоритм рисования линии - необходим на этом проекте для корректной работы детектора коллизий (это внутренний термин, обозначающий ситуацию, когда трактор - если он не поменяет траекторию движения - заедет на уже обработанную поверхность). Что говорит нам Вики: Алгоритм Брезенхе́ма — это алгоритм, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками. Это один из старейших алгоритмов в машинной графике. Здесь важно понимание того, как рисуются линии на экране планшета, а для этого сам экран нужно представить как некую "таблицу" из строк и столбцов, где каждый диод подсвечивает определенную ячейку, то есть, определенный пиксель. В этом "пиксельном мире" невозможно провести линию "по прямой" в нашем обычном понимании: вместо этого несколько точек пойдут по первому ряду, потом по второму, по третьему и т.д. Получается ступенчатая структура. Рисование таких ступенчатых линий - основа работы детектора коллизий: чтобы он определял местоположение точек на линии и за счет этого "узнавал" о коллизии и предупреждал пользователя. Те, кто работает с графикой должны знать алгоритм островов (он отвечает за "заливку") и алгоритм Брезенхема (он помогает рисовать линии и окружности). Если в вузе изучается предмет "машинная графика", то, по идее, миновать их изучение вы никак не сможете.






