21 Февраля 2019
Reading time: 7 min
Что это такое, зачем вам это знать и как этим пользоваться — на примере наших кейсов.
Для начала давайте в общих чертах разберемся, что такое «методы обнаружения разладки случайных процессов» и зачем вам о них что-то знать. На самом деле, все довольно просто.
«Разладка» в данном случае — это краткий термин для любого изменения вероятностных характеристик в той системе, за которой мы наблюдаем. Обратите внимание: не важно, в лучшую сторону у нас что-то изменилось или в худшую — все равно это называется «разладкой».
Что же такое «случайные процессы»? Это такие процессы, течение которых меняется от случая к случаю, а точный результат его нам заранее неизвестен. В природе это, например, броуновское движение или вариации земного магнитного поля.
Вне «живой природы» примеров не меньше. Самым простейшим может служить работа станка на заводе. Мы планируем изготовить на нем строго определенное количество деталей — это нам известно, а вот сколько из них получатся бракованными — этого мы не знаем, а можем лишь пытаться предугадать максимально точно.
Естественно, всем хочется, чтобы предсказать можно было ход любого случайного процесса. При этом нам вовсе не обязательно делать это со 100%-ной точностью, главное, чтобы этой точности хватило для принятия некоего оптимального решения.
QUOTE
К счастью, как пишут Чамберс и Уилер в своем «Статистическом управлении процессами»: «все системы и все процессы очень болтливы. Они хотят рассказать нам о том, как устроены. Проблема в том, что разговаривают они на своем языке, который надо научиться понимать». Для этого нам как раз и нужны «методы обнаружения разладки», это наш инструмент.
Именно методы обнаружения разладки случайных процессов подскажут нам, сколько выпустить деталей, чтобы, с учетом брака, мы поставили заказчику нужное количество. Например, если ему требуется 100 деталей, а мы знаем, что 5% из партии наш станок бракует, то сразу планируем, что произвести нужно минимум 105 деталей (а лучше 106).
И как уменьшить брак, когда заняться техобслуживанием станка (даже если на вид он как новенький). На все эти вопросы отвечают цифры, метрики, случайные величины, за которыми мы наблюдаем.
Стоит отметить, что «станок» — это простой и довольно грубый пример. Методы обнаружения разладки случайных процессов широко применяются в таких сложных областях, как медицинская диагностика и информационные технологии. У программной системы, как и у станка, есть набор метрик — и там, и там можно обнаруживать разладки.
В программировании методы обнаружения разладки — это не только инструмент, но и своеобразное напоминание о том, что в системе всегда может что-то случиться, пойти не так. Это не очевидно, но легче писать программу исходя из того, что в ней будут случаться разладки, нежели считая, что она будет «просто работать».
Целиком весь комплекс наблюдений с помощью методов обнаружения разладки случайных процессов называется «наблюдаемостью системы» (это одно из свойств управляемых систем). В любом случае эти методы направлены на наблюдаемость системы, они позволяют вскрывать факты того, что система стала работать по-другому, хотя мы внешне пока еще никакими факторами это отследить не можем.
Пример наблюдаемости системы в нашей жизни
Давайте рассмотрим небольшой развлекательный пример того, как методы обнаружения разладки мы можем использовать в областях, на первый взгляд вообще никак не связанных с математикой.
Существует такой фильм, «Moneyball», который при переводе на русский язык назвали «Человек, который изменил все», вышедший в 2011 году. Фильм снят по книге Майкла M. Льюиса, изданной в 2003 году, о бейсбольной команде «Окленд Атлетикс» и её генеральном менеджере Билли Бине. Его целью было — создать конкурентоспособную бейсбольную команду, несмотря на банальное отсутствие денег.
Суть фильма в том, что «Окленд Атлетикс» — самая бедная команда в лиге, а результат она все равно должна показывать. Менеджер этой команды, которого играет Бред Питт, знакомится с экономистом из Йельского университета, который предложил необычную методику «победить» с помощью математических рассчетов. Вместе они посчитали сколько и каких результативных действий делают все игроки в команде, когда эта команда побеждает. На основании расчетов, в «Окленд Атлетикс» стали подбирать не дорогих супер-звезд, а самых «завалящих» игроков, но таких, которые суммарно могут обеспечить нужный результат: кто-то хорошо играет на определенной позиции, кто-то хромой/кривой/слепой, но отлично бьет, кто-то совсем новичок, но владеет неким финтом и пр. Благодаря верным расчетам, эта команда действительно выиграла регулярный чемпионат.
Мораль правда в том, что их «вынесли» в первом же раунде плей-офф. Почему? Потому что там играют звезды. А чем звезды отличаются от таких игроков? В регулярном чемпионате команда главного героя играла на максимуме КПД и больше ничего «предъявить» соперникам уже не могла, а звезды просто в момент плей-офф резко и запредельно увеличивает свой КПД.
Этот фильм как раз очень наглядно иллюстрирует понятие «наблюдаемость системы» и показывает, как и по каким характеристикам можно судить о ее развитии, вести статистический учет. В целом, статистика в спорте применяется очень активно как отдельное направление, а здесь мы видим простой и наглядный пример того, как это работает.
Далее поговорим о том, откуда эти «методы обнаружения разладки случайных процессов» взялись и как они вообще работают.
Экскурс в историю
Наша история начинается в Америке 20-х годов, где семимильными шагами шли работы по телефонизации. Корпорация American Telephone and Telegraph (АТ&Т) повсеместно внедряла телефоны, а ей на пятки наступали конкуренты. Чтобы как-то от них отстроиться, компания объявила, что будет устранять любые неисправности в течение суток.
Главным источником всех поломок были ламповые усилители сигнала. Полупроводники тогда еще не изобрели, а лампы, невзирая на свои гарантийные сроки, регулярно ломались.
Руководители компании никак не могли понять, сколько же им вообще нужно содержать аварийных бригад, чтобы вовремя производить ремонт.
Как пишут авторы «Статистического управления процессами», компания АТ&Т обратилась за помощью в исследовательский центр, созданный А. Беллом специально для таких целей. Вопросом вариабельности моментов, когда отказывали лампы, занялся молодой инженер-физик Уолтер Шухарт. И он не только нашел ответ на сакраментальный вопрос «Сколько нужно аварийных бригад АТ&Т, чтобы поменять лампочку?», но и совершил революцию в представлении о свойствах систем, создал концепцию статистического мышления и предпосылки для современных систем менеджмента качества.
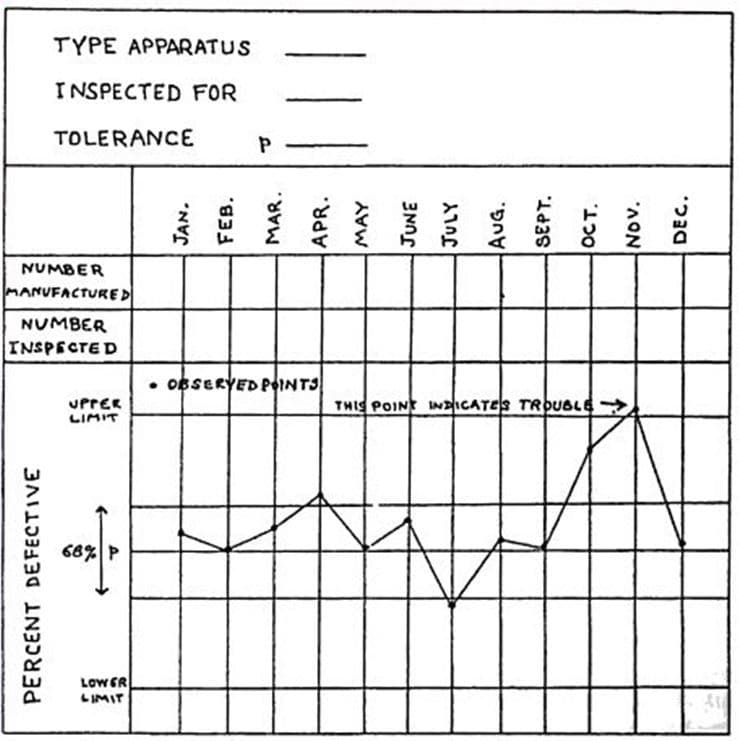
Так появились контрольные карты Шухарта — они как раз и являются способом «перевода» информации о процессе на человеческий язык. Это своего рода инструмент, с помощью которого мы можем «общаться» с процессами и понимать их. А еще — это «прародитель» методов обнаружения разладки случайных процессов. В чем суть?
Шухарт выяснил, что система, если она находится в стабильном, управляемом, устойчивом состоянии, ведет себя так, что ее результаты можно предсказывать с определенной точностью, пока что-то или кто-то не выведет ее из равновесия. Это называется «статистически управляемая система». Предсказуемость системы очень важна, она позволяет управлять процессом, а значит — улучшать его. И наоборот, если есть какие-то вмешательства в систему извне, то о предсказаниях можно забыть.
Система становится не только непредсказуемой, но и неуправляемой. Тогда надо как можно быстрее выявить и устранить источник внешнего вмешательства и вернуть ее в управляемое состояние. Дело за малым. Нужно научиться различать состояния, в которых находится система, а затем решать, что и кому надо с ней делать (или не делать).
Карты Шухарта как раз и отвечают на вопрос: надо или не надо вмешиваться в систему? И если надо, то кому и каким образом?
В общем, Уолтер Шухарт стал первым, кто опубликовал работы, посвященные задаче скорейшего обнаружения разладки и, по сути, придумал методы обнаружения разладки.
Но у его работ был изъян — в них почти нет теоретических выкладок. Шухарт представил набор формул, по которым можно рассчитывать верхние и нижние границы вариабельности системы, но эти формулы всегда подергались критике, потому что в теории вероятности нужно знать, каким распределением обладает случайная величина, чтобы говорить о свойствах этой случайной величины. А у Шухарта подход был совершенно эмпирический и ничего подобного не требовалось, в его методах важно было только то, насколько достоверны результаты и насколько им можно доверять.
Поскольку строгой теории Шухарт не построил, его работы раскритиковали. Однако «знамя обнаружения разладки» быстро подобрали другие ученые. Спустя 20 лет, в 50-х годах вышли труды британского академика Юэна Пэйджа, который предложил методы обнаружения разладки уже опираясь на фундамент теории вероятности.
Этот метод, который впоследствии назвали «метод кумулятивных сумм», основанный на последовательном вычислении функции правдоподобия, оказался удобным и эффективным.
Примерно в то же время советский математик Андрей Николаевич Колмогоров поставил задачу о скорейшем обнаружении момента разладки для винеровского процесса (это как раз математическая модель броуновского движения, которое мы тут уже упоминали). Эта задача была решена советским (и сейчас давно уже российским) математиком Альбертом Ширяевым, который нашел в указанной ситуации оптимальный метод обнаружения.
Как работают методы обнаружения разладки?
Мы уже упомянули, что все, происходящее вокруг нас можно описать некоторым случайным процессом (его еще называют вероятностным или стохастическим). Течение этого процесса может быть различным, в зависимости от случая, а также для него определена вероятность того или иного его течения.
Множество случайных явлений, которые существуют в природе, являются функциями времени. В заданный момент времени величина случайного процесса является случайной величиной. Таким образом, случайный процесс можно рассматривать как случайную величину, индексируемую неким параметром.
Так или иначе, любая величина, которую мы измеряем, в математике называется случайной: мы получаем какие-то ранее неизвестные нам значения. Если измерения происходят регулярно — эти значения постоянно меняются, причем на первый взгляд — хаотично, получается то одно число, то другое.
Но на самом деле у того, какие значения выдает нам процесс, у этой случайной величины, есть характеристики и статистические закономерности, которые определяют, почему именно такие значения она принимает и как с ними можно работать.
В частности, есть такие понятия как плотность распределения случайной величины, характеристическая функция случайной величины. Все это способы задания распределения вероятностей — закона, описывающего область значений случайной величины и вероятности их появления.
Таких характеристик много. И если у нас есть процесс, описанный случайными величинами, то мы, зная эти характеристики, можем выявлять какие-то закономерности.
Что делают методы обнаружения разладки? Они пытаются понять эти закономерности и отследить изменения. Речь идет о том, что если какой-то фактор влияет на случайный процесс, то он начинает идти по-другому, а значит какое-то из свойств случайной величины должно поменяться. В понятии «методов обнаружения разладки» настало время обратить внимание на слово «обнаружение»: эти методы как раз пытаются обнаружить факт того, что характеристики случайной величины изменились.
Для непосвящённого это обнаружение воздействия может быть похоже на магию. Но на самом деле мы просто по этим косвенным наблюдениям понимаем, что характеристики случайной величины меняются и какое-то воздействие стало причиной изменения.
Обратите внимание: методы обнаружения разладки не рассказывают, что произошло. Они только информируют нас о факте воздействия, а дальше людям предстоит потрудиться, чтобы определить, что это было. Впрочем, сопоставляя и анализируя различные возмущения в системе и события, которые происходят, можно все-таки отыскать закономерности.
Самое интересное в этих методах то, что внешне система, возможно, еще никак свое поведение не поменяла, но уже произошли какие-то изменения, события, возмущения внутри, которые в будущем (возможно, в ближайшем) повлияют на внешнее поведение системы. Прелесть в том, что мы можем это обнаружить еще до того, как внешнее поведение изменилось.
Какие бывают методы обнаружения разладки?
Известные методы обнаружения разладки случайных процессов можно разделить на две группы: методы апостериорного обнаружения и последовательные методы.
При апостериорном обнаружении предполагается, что в процессе в некоторый момент произошло изменение характеристик. И, чтобы оценить момент этого изменения, мы собираем всю информацию о процессе, все результаты наблюдений «в кучу». И делаем выводы по результатам всей этой информации в целом.
Последовательные методы основаны на том, что на каждом шаге наблюдения за процессом мы используем всю информацию, полученную на предыдущих этапах. И на основе этой информации либо принимается решение о наличии разладки, либо — о продолжении наблюдений. Соответственно, при использовании этого метода возникает запаздывание в обнаружении разладки.
При обнаружении обоих методов также появляются две возможные ошибки:
- Ложная тревога, когда решение о наличии разладки принимается в ее отсутствие.
- Ситуация, когда разладка есть, а мы считаем, что ее нет.
Основные характеристики последовательных методов обнаружения разладки случайных процессов — это среднее время между соседними ложными тревогами и среднее время запаздывания при обнаружении разладки. Совершенствование методов обнаружения разладки как раз идет по двум направлениям — либо уменьшать количество ложных срабатываний, либо уменьшать количество моментов, когда мы пропускаем важные изменения системы.
Достаточно хорошо изученной к настоящему времени является задача обнаружения изменения распределения в последовательности случайных величин. Для решения этой задачи применяются методы скользящего среднего, экспоненциального сглаживания, кумулятивных сумм.
К настоящему времени разработан также ряд методов обнаружения моментов разладки случайных процессов с зависимыми значениями. Часто в качестве моделей наблюдаемых процессов используются процессы авторегрессионного типа, которые позволяют при небольшом числе параметров хорошо аппроксимировать корреляционную функцию.
Во многих случаях задача обнаружения момента разладки случайных процессов оказывается тесно связанной с задачей оценивания параметров этих процессов. Для оценивания неизвестных параметров процессов авторегрессионного типа применяются методы наименьших квадратов, максимального правдоподобия, стохастической аппроксимации.
Свойства получаемых оценок изучаются в асимптотике, при неограниченном увеличении объема наблюдений. Это позволяет установить скорость сходимости оценок к истинным значениям параметров, а также найти предельное асимптотическое распределение оценок.
Наши кейсы
О том, как мы использовали карты Шухарта, чтобы определить эффективность интернет-тролля на новостном портале, можно почитать здесь.
О том, как с помощью карт Шухарта студенты смогли в 10 000 раз сократить количество ошибок в новой версии системы по сравнению со старой, написанной опытными программистами, читайте тут.
О том, как с помощью карт Шухарта увидеть, как повсеместно обманывают менеджеров по продажам — узнаете, читая блог. Материал в разработке и скоро появятся.
Список использованной литературы:
«Статистическое управление процессами: Оптимизация бизнеса с использованием контрольных карт Шухарта». Дэвид Чамберс, Дональд Уилер.
Диссертация «Последовательное обнаружение моментов разладки случайных процессов», автор — Воробейчиков Сергей Эрикович. Томск, 2000 год.
Персоналии в тексте:
Уолтер Шухарт, американский ученый, получил докторскую степень по физике, но прославился как «отец статистического управления качеством»;
Юэн Стаффорд Пэйдж, британский академик и ученый в области компьютерных наук;
Альберт Николаевич Ширяев, советский и российский математик, академик РАН.
Читайте также